இது தொடர்பில் உடனே கவனம் செலுத்தினால் மக்களுக்கு பயனுள்ளதாக இருக்கும்
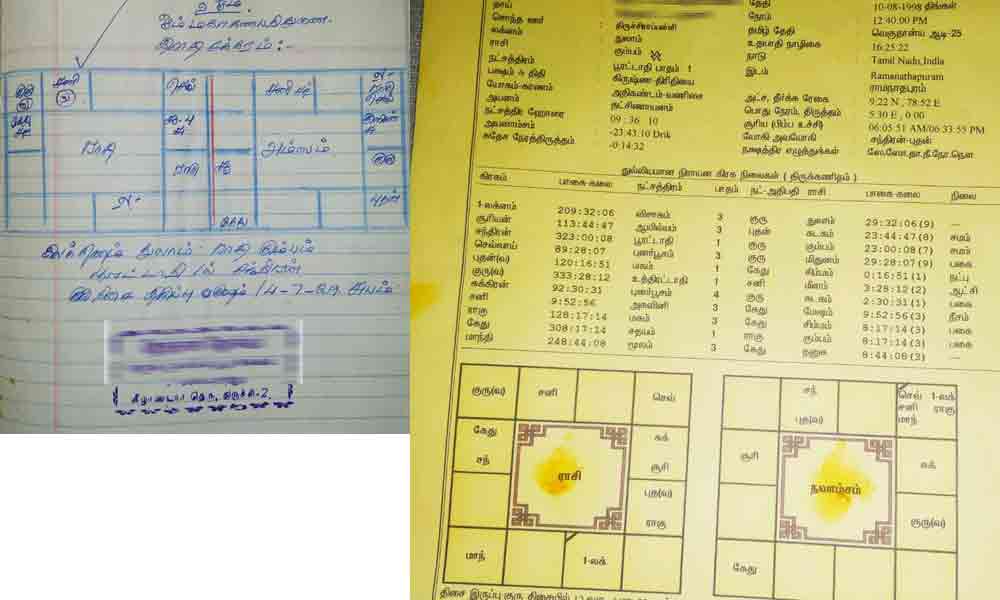
தமிழ் ஆருடம் - ஜோதிடம்
நம் தமிழ் மரபில், பல ஆன்மீக நம்பிக்கைகள், ஆழ்ந்த அறிவியல் பின்புலம் கொண்டவை என்பதை நாம் பல நேரங்களில் உணர்ந்து இருப்போம்.
சல்லிய தோஷம் என்று பெயர் வைத்துள்ளனர். இது ஜாதக தோஷம் இல்லை. வாஸ்து முறைகளை கணிப்பவர்கள் இப்படியான ஒரு தோஷத்திற்கு வழி இருக்கிறது என்கின்றனர்.
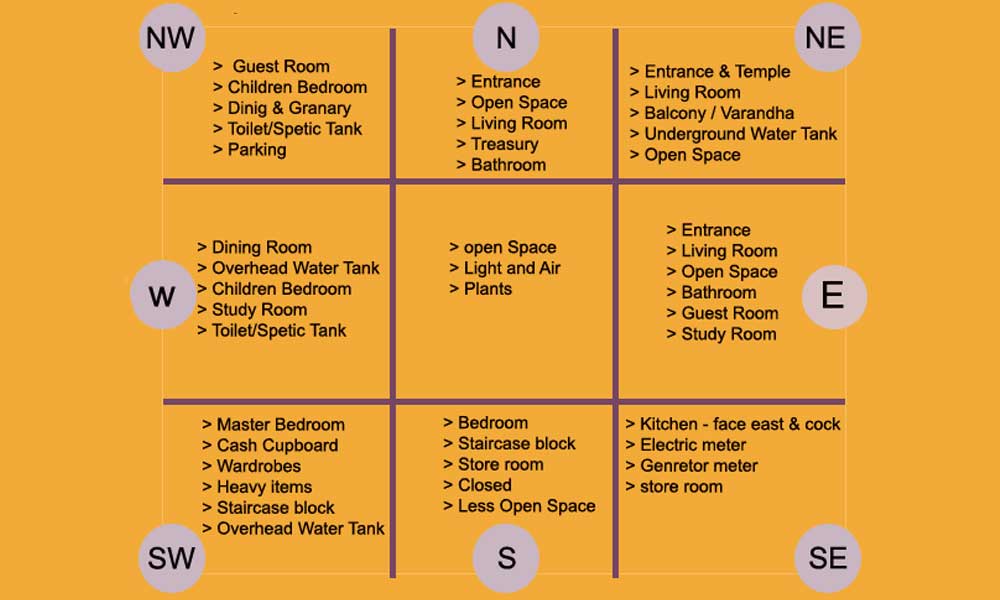
வாஸ்து குறிப்புகள்
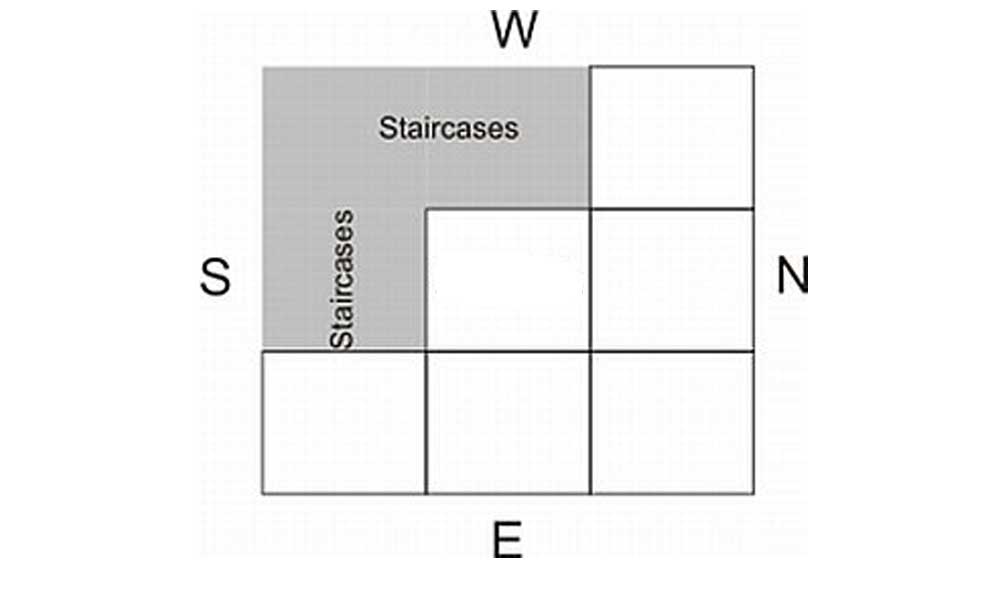
வடகிழக்கு மூலையில் அமையப்பெற்ற படிக்கட்டு பொருளாதார இழப்பையும் தன்மான இழப்பையும் ஏற்படுத்தும்
அதே ஊரில், அதே தெருவில், மற்ற ஒருவர் அதே தொழிலை சிறப்புடன் செய்து தொழில் வெற்றி பெருகிறார்.
உழைத்து ஈட்டிய செல்வத்தை சேர்த்து வைக்கவும், தலைமை படுக்கை அறையை அமைக்கவும் சிறந்த மூலை குபேர மூலை என்றழைக்கப்படும் தென் மேற்கு மூலை பகுதியாகும்.
தமிழகத்தின் ஆகம விதி என்பதே சிவாலயங்கள் எப்படி கட்ட வேண்டும், சாமி எந்த சிசையில் இருக்க வேண்டும் என்பதற்கான விதி தான்.